Mathematics Counts: The Cockcroft Report (1982)

I've just found that the entire text of this report can be found here; it may well be 30 years old but it seems as fresh and relevant as ever. I thought I would reproduce paragraph 243 below to make it even easier to find it:

"243 Mathematics teaching at all levels should include opportunities for


exposition by the teacher;

discussion between teacher and pupils and between pupils themselves;

appropriate practical work;

consolidation and practice of fundamental skills and routines;

problem solving, including the application of mathematics to everyday situations;

investigational work. "

More to come.

Concepts of Area; or: how to link parallelograms and rectangles

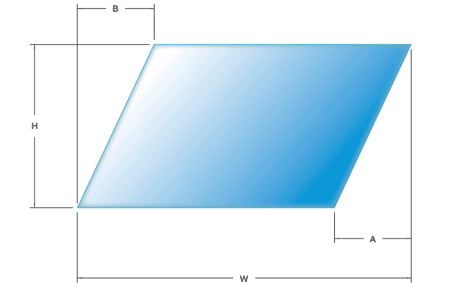
The year 7 teachers have this week been doing some work on the links between the area of a parallelogram and the area of a rectangle with the same dimensions.  This has caused issues for a number of learners, most notably when trying to calculate the height of the shape.  Spending time drawing and cutting up rectangles and parallelograms has proved fruitful but has taken longer than a lot of the teachers expected. We also found that the phrasing of the question also made a big difference to learners' attempts: "Does the rectangle fit inside the parallelogram?" led to a much different exercise than "Who can do it in the fewest cuts?".

Whilst observing a class who had been given a sheet of one 8cm x 4cm rectangle and three 8cm x 4cm parallelograms, I was struck by the necessity of there being some forcing of awareness to make sure that connections between concrete and abstract forms were made.  Learners set about measuring the sides of both the rectangles and the parallelograms getting 32 square cms for the rectangle and other answers for the parallelograms. Learners then set about cutting up the rectangle to fit it over one of the parallelograms; some very proficiently. However, at this point I noticed that conversation had changed to who had done it in the fewest cuts and the implications of the rectangle fitting perfectly were not being appreciated.

It occured to me that some stages need to be moved through in order for there to be a deep understanding:

-Establish clearly the area of a rectangle (what it means and how to find it)
-Make predictions of what you think the areas of the parallelograms will be
-Use concrete forms to rearrange one or the other area
-establish what the implications from the concrete forms are
-think about whether the original predictions need to be altered in the light of the implications.

Discussion and Follow up in the Mathematics Lesson

Some of the difficulties that teachers have reported at the beginning of using Big Ideas has been what to do after a class has had a discussion, what to do to ensure that a discussion has been a fruitful activity. Whilst believing that the act of taking part and engaging in a discussion in a mathematics lesson is positive and important in itself, I shared their concerns.


For those of you who have been similarly unsure I thought it would be helpful to share some of the ideas that I suggested with you on the blog:


1)Ask the learners to do some writing based upon their experience of the discussion: what have they learnt that they did not know before? What did they think before? What did other people think?

2)  Ask learners to summarise the debate for someone who wasn't there (and then pick and share some of them). Reading which points were important to different learners can highlight a lot for the teacher.

3) Be sure to leave enough time at the end of the lesson for there to be a shift in mode of working, i.e. you might be expecting the learners to go from sitting in a circle discussing as a whole group to sitting and writing reflectively on their own. This require both a physical and mental shift and requires some effort.


4) Be prepared to answer questions about what form the responses should take but give other learners the opportunity to make suggestions as well.

How do you frame discussion in your lessons? What do learners do after discussing? What do you think of these suggestions? Leave a message...

Big Ideas Released

 My first publication has just been published with the ATM and is now shipping. Apologies about the delay of the CD but if you've already received the book you should receive the CD this week.

I am really excited to hear from those of you who have picked up the book and have started using some of the ideas. Please leave a comment below to let myself and others here about any successful lessons or possible pitfalls that you have had.

Looking forward to working with you all!

Dan Meyer: Math Class needs a makeover

A really exciting talk about the damage we do in 'helping' our students; and the changes we can make to encourage our learners to become self-motivated and independent.

The 'tweaking' of mathematical tasks is a stand-out topic in this talk and lead me to reflect on the tasks that I give to my learners. Think of a task you have offered a class recently, to what extent did it encourage learners to act on their own initiative?

An Open Way of Working

I was recently asked for some tasks to use with KS3/4 that would help teachers work in a more 'open way'. I decided that it is not so much the task but the way of working itself that is vital. The tasks themselves are what comes after the way of working has been established. Have a look at what I wrote and let me know what you think.

In terms of working in 'this way', I have found that there are a number of intermediary steps required before specific tasks will be of any use. For a start it is important that you are constantly working with your class on 'becoming mathematicians' this can be explicitly stated to students and perhaps discussed. How would a mathematician approach this task? What would a mathematician do that is different from a non-mathematician? These questions, if used consistently and given enough time, can change learners perspectives about what it means to 'do mathematics'.

Other important shifts in practice would include how resources and tasks are used. A task that has the potential to be open and exploratory and interesting for learners can easily be undermined should the teacher fall into the trap of 'telling'. As soon as we are arresting initial considerations, discussions, attempts and ideas and replacing them with 'the way to do it' we might as well not have bothered finding the task. Unfortunately this will mean quite a few lessons where learners are frustrated: if they are used to the teacher being the person who tells them what to do they are going to be annoyed and upset. Some structure towards this way of working is thus needed.

I have found that the easiest way to work like this with a class is to do it from day one. Obviously you don't currently have this luxury (but you soon will!) so this might mean with your current classes building in 10-15 minutes at the start of each task a time where learners are going to try and make sense of the task themselves. You might refuse to answer any questions until then. After this time you could ask the class for any observations: what do they think about the task? What approaches are they considering? What vocabulary do they not understand? This discussion in itself could last another 10-15 minutes. Eventually you might get to the point where the period of initial consideration could last most of the lesson with very little input from you.

Beyond this it is important to find opportunities to empower the learners. Instead of giving them 10 questions all the same, why not give them two and ask them to write their method and then invent 3 more of their own...that way they can answer them and set them for other learners. They could even share them on the board. You will be surprised: learners will often think of far more challenging examples than you would have set them. I really believe that Nrich has more than enough starting points for you to explore with your class but I would say before you use them try them yourself...they are often quite tricky and require some getting used to. Support during this period is not an issue: in fact it is probably vital: what is important is how, over time, this support fades away.

Two final thoughts:

1. There is no such thing as a bad resource, just a bad use of a resource.

2. Don't think with questioning it is as simple as open questions - good, closed questions - bad. The task 'write me a sum with the answer 12' will be a lot less interesting than 'write me a sum which includes at least one negative and at least one decimal and has the answer 12'.

John Taylor Gatto, Dumbing Us Down and Enforced Schooling

I read Dumbing Us Down for the first time this week (Flu and Chest Infection made this possible) and was shocked by how much the ideas within spoke to me.

Gatto's concern is that through forcing children to go to school, to shuffle around to the sound of a bell, to follow instructions, to accept our judgements of them, we are disabling them. We are making students dependent.

Gatto's solutions are radical: claiming that the systems as they are cannot be fixed and need to be destroyed to stop this. I don't know what I think of this being a teacher myself. It's scary.

What I do know however is that every time I reach over to snatch the pen out of a student's hand to complete a task for them, or go to finish their sentence, or presume to second-guess them or begin to interrupt them I will think about the possible effects that is having.